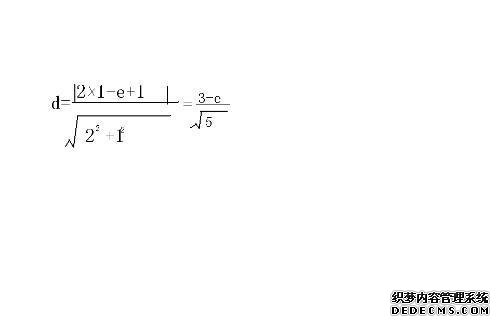1.圆锥曲线范围有两种通用方法。(1)找到一个有效的不等式。通常,和弦△> 0的中点在曲线上。(2)一个数量可以表示为另一个变量的函数,该函数的值的范围。
2.最大值,固定值,圆锥曲线的过固定点等难题。
直线和圆锥曲线之间的位置关系:
(1)从几何角度来看,直线和圆锥曲线之间存在三种位置关系:相分离,切线和交点。相分离意味着在直线和圆锥曲线之间没有公共点,而切线意味着在直线和圆锥曲线之间存在唯一的公共点。直线曲线和圆锥曲线之间有两个不同的公共点。要特别注意直线和双曲线。如果抛物线只有一个公共点,则它不一定是切线,就好像直线平行于双曲线和双曲线渐近线一样。如果该线与抛物线的对称轴平行(一致),则该抛物线有一个公共点,但该线与抛物线相交,因此该线与双曲线和抛物线唯一相关。common是切线或相交,并且线与两条曲线相交。可能有两个交叉点或两个交叉点。因此,直线和曲线的位置不应由公共点的数量确定,而位置关系可以确定公共点的数量。(2)从代数的角度,根据线性方程和圆锥方程的数量,通过组合线性方程l和圆锥曲线方程,位置关系为ax2 + bx + c = 0.1。当a = 0时,它是圆锥双曲线,直线l与双曲渐近线平行或重合。如果圆锥是抛物线,则直线l与抛物线的对称轴平行或重合。对于2Δ0,直线和圆锥曲线在两个不同的点相交。当Δ= 0时,直线和圆锥曲线分别是点的切线和切线。在Δ0的情况下,直线和圆锥曲线没有公共点并且分开。
线与圆锥曲线相交的弦长公式:
如果直线l和圆锥曲线F(x,y)= 0在两个点A和B相交,则链AB的长度可以通过两种方式获得:(1)找到交点法。存在具有圆锥曲线方程式的直线方程,求解点A和点B的坐标,并使用两点之间的距离公式得出链AB的长度。(2)吠陀定理:吠陀定理可以不用吠陀定理来求解,而是用y = kx +或x = n表示直线l的方程。
以上内容是Magic Square的学习社区(www。
Mofunge
Com)未经许可不得播放原始内容!